前回のお話が一番簡単な揚力の発生プロセス
「とりあえず板を傾ければOK」ってお話でした、
「もう少し予算使って性能を上げましょう」ってお話です
何事も「経済対効果」ってヤツが付いて廻るのはこの世の常、
もっと効率よく飛ぶ為の「翼型」を見てみましょう
えーーこれが翼型です。
まぁ、、お馴染みの形ですよね 裏返して使えば車のウイングです
各部分の名称から説明します
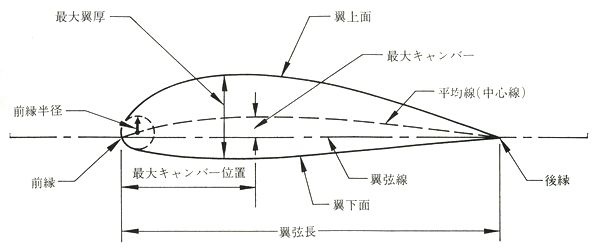
①前縁(ぜんえん)翼型の前側 先端の名称です
②後縁(こうえん) 翼型の後ろ側 後端の名称です
③翼弦線 前縁と後縁を結んだ直線で、この翼弦線と相対気流の作る角度が迎え角になります
③中心線 翼型の厚さ方向の中心を結んだ線で翼型の反り具合(キャンバー)を表します
④最大翼厚 翼の最厚い部分です
調べればいくらでも出てきますが、まぁ、この程度で十分です、
翼型による大まかな特徴は
①翼厚が大きいと低速向け 同じ迎角でも揚力が大きい、同時に抗力も大きい
②キャンバーが大きいと低速向け 同じ迎角でも揚力が大きい、同時に抗力も大きい
まぁ、見たまんまのイメージですね
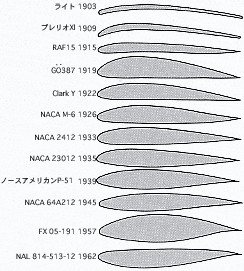
翼型の歴史を見てみると
一番上のライトフライヤーやブレリオまでは板を
「とにかくこーすると飛べるッぽい」って単純に曲げた感じ
基本的に凸カーブを描くと流れる流速が増してベルヌーイの定理(連続の法則)により圧力が低下するので、翼上面は凸カーブを描き
逆に凹形状のカーブになると減速するので圧力が上昇するので下面は凹カーブになります
初期の翼型は上面が凸カーブで下面が凹カーブ、
初期のエンジンなので出力も低く重いので「とにかく低い速度でも大きな揚力を取り出す」って考え方
Clark Y(クラークY)でほぼ下面が平らな形状、
これ以降から翼の下側も膨らみ始めて高速化が進みます。
なんで下面を凸カーブにすると高速化なのか?って、、、
揚力の式にその答えがあって
速度Vは2乗に作用するので
速度が2倍になると揚力は4倍
贅沢な話、高速化が進むと揚力が余っちゃうんです(笑)
だから、高速化が進むほど下の凸カーブが膨らみ、上下の流速差が小さくなります。
ただし離着陸には「低い速度で大きな揚力」が必要になるのでフラップやスラットが追加されるって話です。
さらに高速用の翼型になるともはや下面のカーブの方が大きい、、、
ここまで来ると僕にもわかりません そんな速い飛行機飛ばさないし(笑)
ここは「飛行機を設計する頭の良い人」がウンヌン悩むところなので、
「飛行機を使う人」は悩んでもしょうがないので軽く流します
いくらパイロットが悩んでも出来上がった飛行機の翼は変更できませんから
「翼型にすると何が良くなるの?」って
平板の問題点を並べて見ると
①相対気流が迎角を持った平板に当たった時に生する抗力(空気抵抗)は発生する揚力に対して大きく効率が悪い
②迎角が大きくなった場合にきれいに翼に沿って曲がらす翼の上面から剥離しやすい
翼の上面から相対気流が剥離すると渦が発生し
この渦により抗力が一気に増え揚力が減少します。
この現象を失速って言います。
平板に比べ翼型は、
①流線型で非対称形状にする事で迎角が小さい状態で大きな揚力を生むので抗力(空気抵抗)が小さくなる
②滑らかに相対気流が表面を流れるようになり大きい迎角まで剥離(失速)を遅らせます。
翼型の目的は翼の効率を高める事であり
翼の効率は揚抗比(L/D)で表されます。
ベルヌーイの定理を後にしたのは
ベルヌーイの定理の流速による圧力変化だけでは背面飛行の説明が出来ないんです。
だって翼面のカーブだけで発生する揚力の向きが決まってしまうので裏返しにすると絶対に飛べないって事になりますし。
カーブ無い平板は揚力が発生しないって事になります。
基本はあくまでも相対気流と迎角により発生する圧力差であり
高効率&高速化により翼型が進化したと考えます。
さて、、、ここまで書いてスッキリしないのが
「ベルヌーイの定理」
学生の頃に習ったベルヌーイの定理による揚力の説明は
「翼に相対気流が当たると空気は前縁で上面と下面に別れて後縁で同時に合流する
このときに上面は凸カーブを描くので移動距離が長くなり流速が高まり圧力が減少する」
って事でしたが
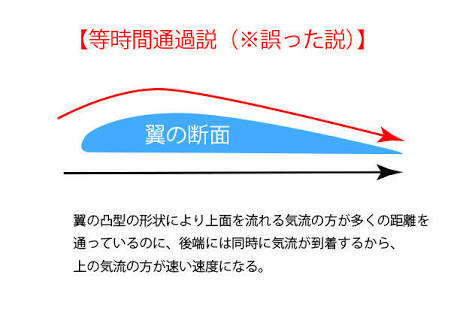
実験してみると、同時に合流しない
どちらかといえは上面の方がより速く流れているらしいです。
そもそも同時に合流しなきゃならない理由も無いよね(笑)
色々と調べていますが、上面で流速が高まる理由が上手く説明出来ないのでスッキリしません、、、
ブログランキングに参加しています、記事を気に入っていただけましたら
↓クリックしていただけると嬉しく思います。
![]()
にほんブログ村
![]()
飛行機ランキングへ

